环形链表

发表于 更新于 分类于

LeetCode题目环形链表集合
环形链表I
环形链表II

环形链表I

题目描述：给定一个链表，判断链表中是否有环。
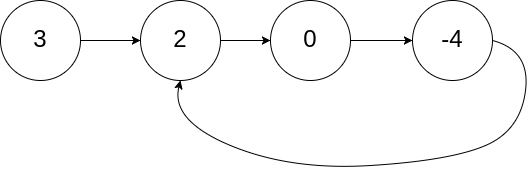
样例输入：head = [3,2,0,-4]
输出：true

思路1-快慢指针

从给定的头指针开始，设立两个快慢指针，快指针fast每次走两步(fast->next->next),慢指针slow每次走一步(slow->next)，如果存在环，最终必定相遇。
如果fast和slow指针走的过程中遇到NULL,说明其中没有环,返回false。
如果fast和slow指针相遇(不全为空),说明其中有环,返回true。

AC代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == NULL || head->next == NULL) return false;
        ListNode *fast = head, *slow = head;
        while(fast->next != NULL && fast->next->next != NULL)
        {
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow) return true;
        }
        return false;
    }
};

思路2-修改next指针

遍历整个链表，每遍历到一个对象，将其next指针指向自己。
过程中遇到next为NULL, 说明其中没有环，返回false。
过程中遇到next指向自己, 说明其中有环，返回true。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == NULL || head->next == NULL) return false;
        ListNode *nextp=head;
        while(head != head->next)
        {
            if(head->next == NULL) return false;
            nextp = head->next; 
            head->next = head;
            head = nextp;
        }
        return true;
    }
};

需要说明的是这种方法会改变原来链表的结构，实际中并不可取。

环形链表II

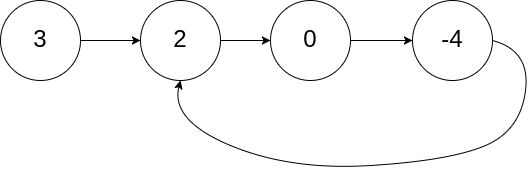
题目描述：给定一个链表，判断链表中是否有环，如果有环，返回进入环的第一个节点，如果无环，返回空。
题目要求：尽量不使用额外空间，不允许修改链表。


思路分析

  1. 先用环形链表I的方法，判断链表中是否有环，如果有环，得到fast指针和slow指针的位置。
  2. 再使slow指针指向head, fast指针指向第一步slow和fast的相遇节点地址。
  3. 使fast和slow均以一步(.next)的方式向前走，相遇的地方即是需要返回的节点。

注 第三步的证明可以看Leetcode官方题解。

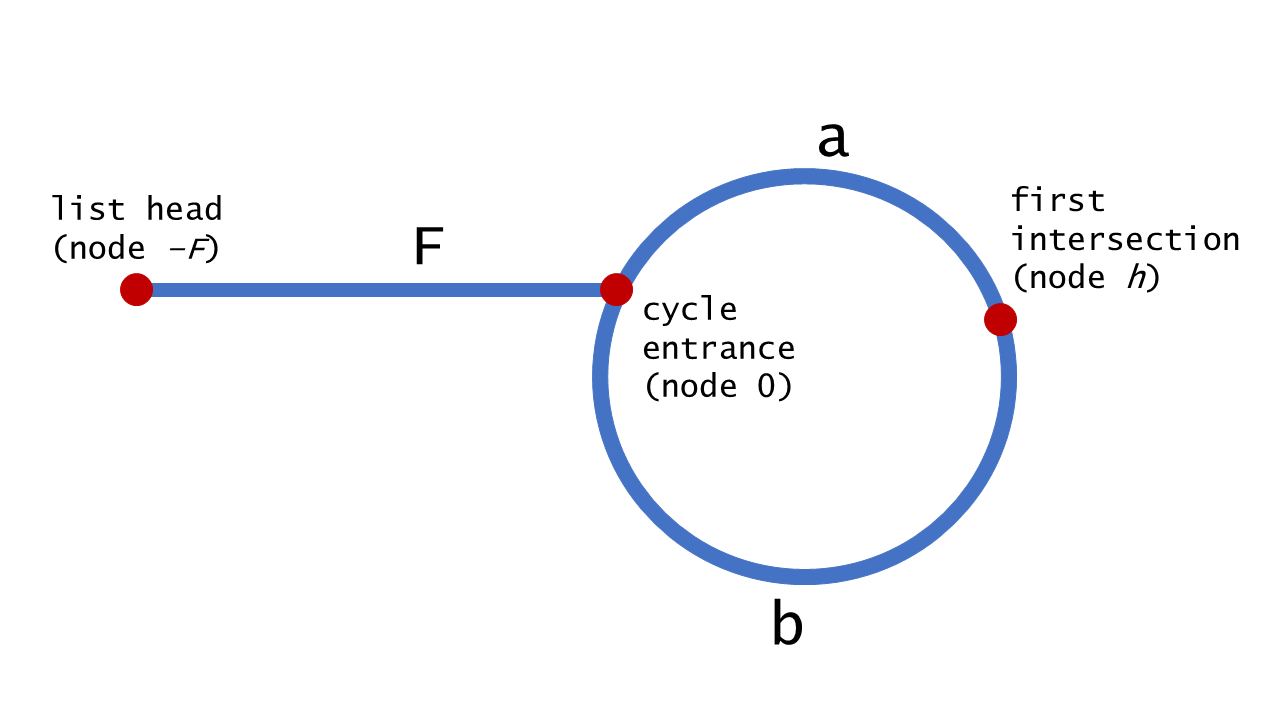
2*(F+a) = F + n*(a+b) + a –> F = (n-1)(a+b) + b –> F = b

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) { 
       if(head == NULL || head->next == NULL) return NULL;
        ListNode *fast = head, *slow = head;
        while(fast->next != NULL && fast->next->next != NULL)
        {
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow) break;
        }
        if(!(fast->next != NULL &&fast->next->next != NULL)) return NULL;

        
        slow = head;
        while(fast != slow)
        {
            fast = fast->next;
            slow = slow->next;
        }
        return fast;
    }
    
    
};

寻找重复数

比如包含8个整数的数组，元素都在1-7之间。我们发现数组的下标的范围是0-6，如果把数组中每个元素的值看做记录的是下一个数的地址，那么就会构成一个链表。而且此链表必定有环。而且环的入口节点的下标就是重复的元素。

所以可以利用快慢指针来做

AC代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int fast=nums[0],slow=nums[0];
        while(1)
        {
            fast = nums[nums[fast]];
            slow = nums[slow];
            if(fast == slow) break;
        }
        
        fast=nums[0];
        while(fast != slow)
        {
            fast = nums[fast];
            slow = nums[slow];
        }
        return fast;
    }
};